Significance of Octaves and Decades

OCTAVE AND OTHER FREQUENCY INTERVALS

The octave in music

In music, the octave is the interval between two frequencies which are in the ratio of 2-to-1 (i.e. the higher frequency is exactly twice the lower frequency). Check out the following examples.

The complete musical scale is generated by defining one frequency (the note A which is 440 Hz) and working out all of the other musical notes, with sharps and flats etc, from that defined frequency.

The octave in acoustics and audio

In acoustics and audio, the octave is the interval between two frequencies which are in the ratio of 10 0.3 to 1 10 0.3 = 1.995 (Calculator key strokes: [shift] [log] [0] [.] [3] [=] )

The standard octave intervals in acoustics are worked out starting from the Reference Frequency of 1 kHz which is 10 3.0 Hz. The full sequence of frequencies is:

On page 2 there is an image of an octave band graphic equalizer. Look below the sliders for the nominal frequencies listed on the bottom row of the table above.

Fractions of an octave

On the Klark-Teknik graphic equalizer, on page 3, there are two sliders between each of the standard octave sliders. For example, between the sliders at 250 Hz and 500 Hz there is one at 315 Hz and one at 400 Hz. The sliders on this graphic equaliser are arranged at one-third-octave intervals.

For an octave, the ratio is 10 0.3 . The number 0.3 is the exponent (i.e. the power of ten).

We work out an interval which is a given fraction of an octave by taking the same fraction of 0.3

So, for one-third-octave, the exponent is a third of 0.3, i.e. 1/3 × 0.3 = 0.1 and 10 0.1 = 1.2589 .

This table explains how a number of fractions of an octave can be calculated.

Octave bands

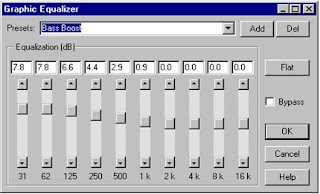
The image below is a graphics user interface (GUI) from some audio-processing computer software and it shows an octave band equaliser. There are 10 octave bands in the audio range; hence 10 sliders.

Below the sliders, you can see the octave interval nominal frequencies *. Each slider controls the gain for a one-octave-wide band of frequencies. The gain, in dB, is shown in the window above each slider.

Each slider=s quoted frequency is at the centre of its respective octave band. The quoted frequency is called the octave band centre frequency. We identify which octave band we are controlling by quoting the octave band centre frequency. Each of the ten octave bands reaches half an octave above the band centre frequency and half an octave below the band centre frequency. So:

the Band Upper Limit is half an octave above (i.e. × 10 0.15) the band centre frequency; and

the Band Lower Limit is half an octave below (i.e. ÷ 10 0.15) the band centre frequency.

For the 500 Hz octave band (shown with a gain of + 2.9 dB in the image):

the exact band centre frequency is 10 2.7 (see page 1 for how this is worked out);

the band upper limit is 10 2.7 × 10 0.15 = 10 2.7 + 0.15 = 10 2.85 = 707.9 Hz

the band lower limit is 10 2.7 ÷ 10 0.15 = 10 2.7 - 0.15 = 10 2.55 = 354.8 Hz

The slider labelled 500 Hz does not adjust the gain only for the frequency of 500 Hz. It adjusts the gain for an octave band of frequencies from 354.8 Hz up to 707.9 Hz. 500 Hz is at the centre of that octave band. The slider adjusts the gain for the whole of the 500 Hz octave band.

The lowest frequency being processed by the software above, is not 31.5 Hz *, but is the frequency at the band lower limit of the 31.5 Hz octave band. (See question 2(e) on page 4.)

The highest frequency being processed by the software is not 16 kHz, but is the frequency at the band upper limit of the 16 kHz octave band. (See question 2(a) on page 4.)

The above image is of an octave band equaliser. The following page shows an example of a one-third-octave band equaliser. The frequency bands are narrower and the EQ control much finer.

(* 31 Hz should be labelled 31.5 Hz; and 62 Hz should be labelled 63 Hz. Many manufacturers get these two wrong.)

One-third-octave Bands

The image below shows a one-third-octave band graphic equaliser. There are 10 octaves in the audio range; so there are 30 one-third-octaves in the audio range.

Each one of the 30 sliders adjusts the gain of the signal for a band of frequencies which is one-third-of-an-octave wide.

These professional equalisers offer fine detailed adjustment to the equalisation (EQ) of the audio signal.

The frequency quoted under each slider is the nominal Band Centre Frequency. So each third-octave band extends from one-sixth of an octave below the band centre frequency to one-sixth of an octave above the band centre frequency. The two extremes are called the Band Lower Limit and the Band Upper Limit.

Notice that the vertical position of the sliders is calibrated in dB with markings at +12, +6, +3, 0, -3, -6, and -12 dB, showing how the power level of each band is increased or decreased relative to the flat response , 0 dB, position.

Decade (log scale)

One decade is a factor of 10 difference between two numbers (an order of magnitude difference) measured on a logarithmic scale. It is especially useful when referring to frequencies and when describing frequency response of electronic systems, such as audio amplifiers and filters.

Calculations

The factor-of-ten in a decade can be in either direction: so one decade up from 100 Hz is 1000 Hz, and one decade down is 10 Hz. The factor-of-ten is what is important, not the unit used, so 3.14 rad/s is one decade down from 31.4 rad/s.

To determine the number of decades between two frequencies, use the logarithm of the ratio of the two values:

How many decades is it from 15 rad/s to 150,000 rad/s?

log10(150000 / 15) = 4 decades

How many decades is it from 3.2 GHz to 4.7 MHz?

log10(4.7x10´6 / 3.2x10´9) = -2.86 decades

How many decades is one octave?

One octave is a factor of 2, so log10(2) = 0.301 decades per octave

To find out what frequency is a certain number of decades from the original frequency, multiply by appropriate powers of 10:

What is 3 decades down from 220 Hz?

220x10´3=0.22 Hz

What is 1.5 decades up from 10?

10x10´1.5=316.23 Hz

To find out the size of a step for a certain number of frequencies per decade, raise 10 to the power of the inverse of the number of steps:

What is the step size for 30 steps per decade?

101 / 30 = 1.079775 - or each step is 7.9775% larger than the last.

Graphical representation and analysis

Decades on a logarithmic scale, rather than unit steps (steps of 1) or other linear scale, are commonly used on the horizontal axis when representing the frequency response of electronic circuits in graphical form, such as in Bode plots, since depicting large frequency ranges on a linear scale is often not practical. For example, an audio amplifier will usually have a frequency band ranging from 20 Hz to 20 kHz and representing the entire band using a decade log scale is very convenient. Typically the graph for such a representation would begin at 1 Hz (100) and go up to perhaps 100 kHz (105), to comfortably include the full audio band in a standard-sized graph paper, as shown below. Whereas in the same distance on a linear scale, with 10 as the major step-size, you might only get from 0 to 50.