Sistema auditivo periférico
El sistema auditivo humano podemos dividirlo en cuatro etapas:
*la fisiológica, de la que se encarga el sistema auditivo períferico.
*la psicológica (percepción) de la que se encarga el sistema auditivo central.
*El Sistema auditivo periférico es el responsable de los procesos fisiológicos de la audición. Estos procesos que permiten captar el sonido y transformarlo en impulsos eléctricos suceptibles de ser enviados al cerebro a través de los nervios auditivos.
*El sistema auditivo periférico lo constituye el oído.
El oído humano se divide en tres partes:
*el oído externo, que canaliza la energía acústica.
*el oído medio, que transforma la energía acústica en energía mecánica, transmitiéndola - y amplificándola- hasta el oído interno.
*el oído interno, donde se realiza la definitiva transformación de la energía mecánica en impulsos eléctricos.
Cuando el sonido llega al oído, las ondas sonoras son recogidas por el pabellón auricular (o aurícula). El pabellón auricular, por su forma helicoidal, funciona como una especie de "embudo" que ayuda a dirigir el sonido hacia el interior del oído.
Sin la existencia del pabellón auricular, los frentes de onda llegarían de forma perpendicularmente y el proceso de audición resultaría ineficaz (gran parte del sonido se perdería):
Parte de la vibración penetraría en el oído.
Parte de la vibración rebotaría sobre la cabeza y volvería en la dirección de la que procedía. (reflexión).
Parte de la vibración lograría rodear la cabeza y continuar su camino. (difracción).
El pabellón auricular humano es mucho menos direccional que el de otros animales (como los perros) que poseen un control voluntario de su orientación. (Los perros pueden mover las orejas a voluntad, los humanos no).
Una vez que ha sido recogido el sonido, las vibraciones provocadas por la variación de presión del aire cruzan el canal auditivo externo y llegan a la membrana del tímpano, ya en el oído medio.
El conducto auditivo actúa como una etapa de potencia natural que amplifica automáticamente los sonidos más bajos que proceden del exterior. Al mismo tiempo, en el caso contrario, si se produce un sonido muy intenso que puede dañar el oído, el conducto auditivo segrega cerumen (cera), con lo que cierra parcialmente el conducto, protegiéndolo.
En el oído medio, se produce la transducción, es decir, la transformación la energía acústica en energía mecánica. En este sentido, el oído medio es un transductor mecánico-acústico.
Además de transformar la señal, antes de que ésta llege al oído interno, el oído medio la habrá amplificado.
La presión de las ondas sonoras hace que el tímpano vibre empujando a los osículos, que, a su vez, transmiten el movimiento del tímpano al oído interno. Cada osículo empuja a su adyacente y, finalmente a través de la ventana oval. Es un proceso mecánico, el pie del estribo empuja a la ventana oval, ya en el oído interno.
Esta fuerza empuja a la venta oval es unas 20 veces mayor que la que empujaba a la membrana del tímpano, lo que se debe a la diferencia de tamaño entre ambas.
Esta presión ejercida sobre la ventana oval, gracias a la helicotrema penetra en el interior de la cóclea (caracol) y pone en movimiento el líquido linfático (endolinfa o linfa) que ésta contiene.
El líquido linfático se mueve como una especie de ola y, transmite las vibraciones a las dos membranas que conforman la cóclea (membrana tectorial, la superior, y la membrana basilar, la inferior).
Entre ambas membranas se encuentra el órgano de Corti, que es el transductor propiamente dicho. En el órgano de Corti se encuentran las células receptoras. Existen aproximadamente 24 000 de estas fibras pilosas, dispuestas en 4 largas filas que son las que recogen la vibración de la membrana basilar.
Como la membrana basilar varía en masa y rigidez a lo largo de su longitud su frecuencia de resonancia no es la misma en todos los puntos:
En el extremo más próximo a la ventana oval y al tímpano, la membrana es rígida y ligera, por lo que su frecuencia de resonancia es alta.
Por el contrario, en el extremo más distante, la membrana basilar es pesada y suave, con lo que su resonancia es baja frecuencia.
El margen de frecuencias de resonancia disponible en la membrana basilar determina la respuesta en frecuencia del oído humano, las audiofrecuencias que van desde los 20 Hz hasta los 20 kHz. Dentro de este margen de audiofrecuencias, la zona de mayor sensibilidad del oído humano se encuentra en los 1000 y los 4000 Hz.
Esta respuesta en frecuencia del oído humano, permite que seamos capaces de tolerar un rango dinámico que va desde los 0 db (umbral de audición) a los 120 dB (umbral de dolor)
El movimiento de la membrana basilar afecta las células del órgano de Corti de forma diferencial, en función de su frecuencia de resonancia. Al ser empujadas contra la membrana tectorial, las células pilosas generan patrones característicos de cada tono o (frecuencia), que al llegar aquí, al final del proceso fisiológico, son idénticas a la sonido original.
En función de estos patrones, al ser estimuladas las células pilosas producen un componente químico que genera los impulsos eléctricos que son trasmitidos a los tejidos nerviosos adyacentes (nervio auditivo y, de ahí, al cerebro), donde se producirá la percepción del sonido gracias al sistema auditivo central.
Las células del órgano de Corti, (células ciliares, capilares o pilosas), no tienen capacidad regeneradora, es decir, cuando se lesionan se pierde audición de forma irremediable. Además, con la edad, desciende la agudeza auditiva de los seres humanos.
La audición Humana
El umbral de audición, para la media de los humanos, se fija en 20 µPa (20 micro pascales = 0.000002 pascales), para frecuencias entre 2KHz y 4KHz. Por encima y por debajo de estas frecuencias, la presión requerida para excitar el oído es mayor. Esto significa que nuestro oído no responde igual a todas las frecuencias (tiene una respuesta en frecuencia desigual). Un tono puro, a la frecuencia de 125 Hz y con 15 dB de nivel, sería prácticamente inaudible, mientras que si aumentamos la frecuencia, hasta 500 Hz, sin variar el nivel de presión, se obtendría un tono claramente audible.

Las líneas discontinuas marcan los niveles de presión necesarios a cada frecuencia, para que el oído detecte (subjetivamente) la misma sonoridad en todas. Esto quiere decir que si reproducimos un tono de 31.5 Hz a 100 dB (NPS), luego otro de 63 Hz a 90 dB y otro de 125 Hz a 80 dB, el oyente dirá que todos sonaban al mismo volumen. En 2 KHz el umbral de audición se fija en 0 dB y a 4 KHz es incluso menor de 0 dB, ya que a 3600 Hz se encuentra la frecuencia de resonancia del oído humano.Por debajo de 2000 Hz y según se va bajando en frecuencia, el oído se vuelve menos sensible.
Los umbrales de audición para frecuencias menores de 2 KHz son: 5 dB a 1 KHz, 7 dB a 500 Hz, 11 dB a 250 Hz, 21 dB a 125 Hz, 35 dB a 63 Hz, 55 dB a 31 Hz. Recuerda que estos dB's son de nivel de presión sonora (NPS o SPL).Por encima de los 4 KHz, el oído es menos sensible, pero no tanto como en bajas frecuencias. Sin embargo, se producen fluctuaciones a frecuencias cercanas, debido a las perturbaciones que produce la cabeza del oyente en el campo sonoro.
Los umbrales de audición son: 15 dB a 8 KHz y 20 dB a 16 KHz Todos los receptores de sonido, tienen un comportamiento que varía con la frecuencia. En el caso del oído humano, sucede lo mismo, ya que se trata el receptor más complicado y (aunque parezca extraño) más eficiente que existe.
El umbral de audición define la mínima presión requerida para excitar el oído. El límite del nivel de presión sonora se sitúa generalmente alrededor de 130 dB, coincidiendo con el umbral del dolor (molestias en el oído).La pérdida de audición de manera súbita, por daños mecánicos (en el oído medio) se produce a niveles mucho mayores. La exposición suficientemente prolongada a niveles superiores a 130 dB produce pérdida de audición permanente y otros daños graves. En acústica, las frecuencias siempre se tratan de manera logarítmica: representaciones, gráficas y demás. El motivo principal es que el oído humano interpreta las frecuencias de manera casi logarítmica.
En el eje de frecuencias de cualquier gráfica de las vistas hasta ahora, las marcas pasan de una frecuencia (p. ej. 1000 Hz) al doble (2000 Hz). La apreciación subjetiva de un oyente será que hay la misma distancia entre un tono de 200 Hz y otro de 400, que entre uno de 1000 Hz y otro de 2000 Hz. Sin embargo la "distancia" en frecuencia en el primer caso es de 200 Hz y en el segundo de 1000 Hz.
SONIDO, FRECUENCIA Y EL OIDO HUMANO
SONIDO
Sonido es cualquier fenómeno que involucre la propagación en forma de ondas elásticas, audibles o casi audibles, generalmente a través de un fluido (u otro medio elástico) que esté generado por el movimiento vibratorio de un cuerpo.
FRECUENCIA
Frecuencia es una medida para indicar el número de repeticiones de cualquier fenómeno o suceso periódico en la unidad de tiempo. Para calcular la frecuencia de un evento, se contabilizan un número de ocurrencias de este teniendo en cuenta un intervalo temporal, luego estas repeticiones se dividen por el tiempo transcurrido.

OIDO HUMANO
El oído humano es capaz de percibir frecuencias entre 20 y 20.000 Hz, aunque va disminuyendo por la edad. Esta respuesta en frecuencia se conoce como audiofrecuencia, pero el espectro sonoro es más amplio.

OSCILADORES
La frecuencia del oscilador fijo es de 170 KHz y la del variable oscila entre 168 y 170 KHz.
Frecuencias audibles de 0 a 2 KHz para ejecutar el instrumento.

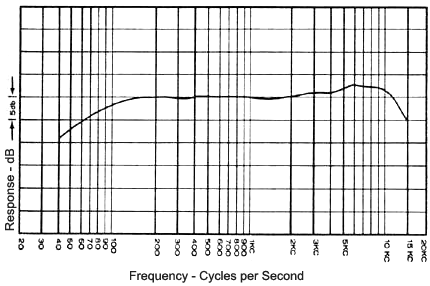
Gráfica de frecuencia.
A la vista de la gráfica se diría que este altavoz tiene una respuesta en frecuencia de 450 Hz. a 4 KHz. con una variación de +/- 3dB....
Caídas de más de10 dB en la respuesta en frecuencia equivale a decir que el aparato no trabaja en esa frecuencia. De este altavoz conocemos a través de la gráfica de respuesta en frecuencia que si se le alimenta con dos señales de igual nivel, una por ejemplo de 800 Hz. y otra de 4000 Hz, la segunda tendrá un nivel de presión sonora (NPS) 6 dB menor que la señal de 800 Hz. Esto significa que reproduciendo música o cualquier otra señal, las frecuencias cercanas a 800 Hz. se escucharán más que las cercanas a 3 KHz.
El caso más favorable (e imposible) de respuesta en frecuencia sería una línea recta que cubra todo el espectro. En este caso hablaríamos de respuesta en frecuencia plana. Como esto es imposible, se suele hablar de la "zona de respuesta plana", aunque realmente se trata de una aproximación. En el caso anterior diríamos que la zona de respuesta plana es la definida entre 800 y 3000 Hz, ya que en esta zona es donde es útil el altavoz.
Zona de respuesta idealmente plana entre 200 Hz y 10 KHz
El oído humano tiene dificultad para detectar variaciones de nivel de presión de menos de 0.3 dB. Esto significa que si exponemos a una persona a un ruido (sonido continuo) y vamos variando el nivel de presión sonora (dando más volumen o menos al ruido), el sujeto notará variación cuando la diferencia de NPS (nivel de presión sonora) antes y después se aproxime a los 0.3 dB. Esto da una idea, de cuanta variación de respuesta en frecuencia es aceptable, por ejemplo en unos altavoces.
Este apartado ha tenido como ejemplo un altavoz; sin embargo todos los aparatos de audio tienen su respuesta en frecuencia característica. En una cadena se sonido, donde la señal pasa por varios equipos uno tras de otro, las respuestas en frecuencia de cada aparato sen van sumando para conformar la respuesta en frecuencia total del equipo completo.
Respuesta en frecuencia de tres sistemas. Representación superpuesta.
La respuesta en frecuencia del conjunto de aparatos será la suma en dB de todas (azul). El amplificador del ejemplo provoca una caída en la respuesta de 6 dB a 6600 Hz y el sistema de altavoces provoca 6 dB de caída a esa misma frecuencia, la respuesta total tendrá una caída de 12 dB en esa frecuencia.
Respuesta en frecuencia total de los tres sistemas en cadena
Como se ha dicho todos los elementos por los que pasa la señal de sonido en una cadena de audio (o una cadena de música) van dejando su huella en el espectro de la señal, recortándola y limitándola. Es por esto que es importante que todos los equipos por los que atraviesa la señal de audio tengan la máxima calidad posible. En cualquier caso todos han de ser de calidad similar, ya que el elemento de peor calidad será el que pondrá el límite a la calidad del conjunto.
Actualmente, gracias al desarrollo de la electrónica, los equipos electrónicos suelen tener una respuesta en frecuencia bastante buena. El punto crítico suele estar en los altavoces, que son elementos mecánicos que no han evolucionado tanto como la electrónica por lo que sigue siendo muy costoso fabricar buenos altavoces. Suelen ser los altavoces los que más limitan la respuesta en frecuencia del conjunto y por lo tanto la calidad del conjunto. Por este motivo en las cadenas domésticas, un parámetro de calidad a tener en cuenta son los altavoces, ya que la electrónica es muy similar en todos los casos.
Otra filosofía muy acertada a la hora de buscar el mejor sonido a base de no modificar el espectro, es desechar todas las etapas en la cadena de sonido que no sean necesarias; ya que por muy buena calidad que tengan, siempre alterarán la señal. Así se explica que los equipos HI-FI más caros y de mayor calidad no tengan funciones como distintos tipos de ecualización, controles de tono, efecto de cine... El motivo es que en estos aparatos de alta gama, la electrónica está cuidada al máximo y ese tipo de funciones "ensucian" la señal, alejándola de la original.
Otro aspecto que no se ha tratado es el tema de la fase. Todos los dispositivos electrónicos modifican la fase y mucho, por esto los equipos HI-FI de alta gama reducen al máximo la electrónica.
Lenny Z. Perez M.
EES
Referencias:
http://es.wikipedia.org/wiki/Sistema_auditivo_perif%C3%A9rico
http://www.estudioveracruz.com/audicionhumana.html
http://nottheremin.wordpress.com/2008/11/09/sonido-frecuencia-y-el-oido-humano/
http://www.sonido-zero.com/biblioteca-de-sonido/grafica-de-frecuencia..html
Get news, entertainment and everything you care about at Live.com. Check it out!






















![[Figura+15.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi_-cRpc7WEuwQcI9ny5XIuDTlTHz_2Rj4xMIe4jJAQIHR92UzxENQ1G5DPgGGe7hAcz82jQkIi5s8TcJ_FWm2EOqloIFnp1XgPLiRXYWQa28gWypUym7xPdmvZotNjE2EtRmzg8BMNktA/s1600/Figura+15.jpg)
![[Figura+16.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi_bfxh9Dok6Nr2BuqX-RoA9RCzFxGaW1_E2qGGMRbzHS_oFCGe6364j7KtZMb3H8sBRVa-ri1A_tRjB-_SWAshCFqUcSGSdkcYmb_tbXLvnYFEmZKmvRvYJ0Vm5xEBDYnyF-51WIoaVTg/s1600/Figura+16.jpg)
![[Ecuacion+14.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiLRbB821INbWn016B93pnTKMu1sro6r2Y3Zjhyphenhyphenwk_y39nnbJAvjM8zINxYpuHKvTb8zRD8wKoqjY8zQxrj2XrrBQQ8F_-Ir75-ihwYq-wcdukiXn1kExcYAjZWCHPtD1pWp-S0ewUW5wk/s1600/Ecuacion+14.jpg)
![[Figura+17.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEidK2KVQBsjRz7upC9rF3uoRowwV_gSMmz-i1UAn9VzsfM4oDZf60Z-Gt3sb5zCq21FkD4_BERy6uw4lWe8N8LlI4tFqPacY84k2adp-VnJ-Pdf0JU6QRm4KZPHnj4DJQd1x05O5Re5Uf8/s1600/Figura+17.jpg)
![[Ecuacion+15.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi6SrxAVs6iUXOfNCOhbi4UX5eFxYRCN8LyyQR8jW4CA2WZqI-tcFshHtzz1fDEDQxCINZ8GnmzHVDM3UxI860xfhWBTLKVgnm2OWLEoUtDmFx_dJuZB5hyphenhyphenqaP9FWqJF_f7sQdgaGU77E4/s1600/Ecuacion+15.jpg)
![[Figura+18.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj6fVBh8Ohjw_ZRNs_hnZJ7QRSFvHk_N6ZYn3Vo6Op7y8wYT1MYpM0n3-9LOgcUgg50xSLvaV1IdhcFPw9AHTDqhFAdXpcrNUi9JEfnOMf4eoAHdkK8ZMEs7-sGP1JRBmXkoux-N2Fy-yQ/s1600/Figura+18.jpg)