Frequency response is the measure of any system's output spectrum in response to an input signal.[1] In the audible range it is usually referred to in connection with electronic amplifiers, microphones and loudspeakers. Radio spectrum frequency response can refer to measurements of coaxial cables, category cables, video switchers and wireless communications devices. Subsonic frequency response measurements can include earthquakes and electroencephalography (brain waves).
Frequency response requirements differ depending on the application.[2] In high fidelity audio, an amplifier requires a frequency response of at least 20–20,000 Hz, with a tolerance as tight as ±0.1 dB in the mid-range frequencies around 1000 Hz, however, in telephony, a frequency response of 400–4,000 Hz, with a tolerance of ±1 dB is sufficient for intelligibility of speech.[2]
Frequency response curves are often used to indicate the accuracy of electronic components or systems.[1] When a system or component reproduces all desired input signals with no emphasis or attenuation of a particular frequency band, the system or component is said to be "flat", or to have a flat frequency response curve.[1]
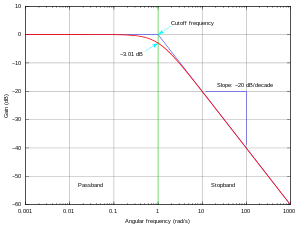
Frequency response of a low pass filter with 6 dB per octave or 20 dB per decade
The frequency response is typically characterized by the magnitude of the system's response, measured in decibels (dB), and the phase, measured in radians, versus frequency. The frequency response of a system can be measured by applying a test signal, for example:
§ sweeping a constant-amplitude pure tone through the bandwidth of interest and measuring the output level and phase shift relative to the input
§ applying a signal with a wide frequency spectrum (for example digitally-generatedmaximum length sequence noise, or analog filtered white noise equivalent, like pink noise), and calculating the impulse response by deconvolution of this input signal and the output signal of the system.
These typical response measurements can be plotted in two ways: by plotting the magnitude and phase measurements to obtain a Bode plot or by plotting the imaginary part of the frequency response against the real part of the frequency response to obtain a Nyquist plot.
Once a frequency response has been measured (e.g., as an impulse response), providing the system is linear and time-invariant, its characteristic can be approximated with arbitrary accuracy by a digital filter. Similarly, if a system is demonstrated to have a poor frequency response, a digital oranalog filter can be applied to the signals prior to their reproduction to compensate for these deficiencies.
Frequency response measurements can be used directly to quantify system performance and design control systems. However, frequency response analysis is not suggested if the system has slow dynamics.[citation needed]
The frequency response of an LTI filter may be defined as the spectrum of the output signal divided by the spectrum of the input signal. In this section, we show that the frequency response of any LTI filter is given by its transfer function  evaluated on the unit circle, i.e.,
evaluated on the unit circle, i.e.,  . We then show that this is the same result we got using sine-wave analysis in Chapter 1.
. We then show that this is the same result we got using sine-wave analysis in Chapter 1.
Beginning with Eq. (6.4), we have
(6.4), we have
where X(z) is the z transform of the filter input signal  ,
,  is the z transform of the output signal
is the z transform of the output signal  , and
, and  is the filter transfer function.
is the filter transfer function.
A basic property of the z transform is that, over the unit circle  , we find the spectrum [84].8.1To show this, we set
, we find the spectrum [84].8.1To show this, we set  in the definition of the ztransform, Eq.
in the definition of the ztransform, Eq. (6.1), to obtain
(6.1), to obtain

which may be recognized as the definition of the bilateral discrete time Fourier transform (DTFT) when  is normalized to 1 [59,84]. When
is normalized to 1 [59,84]. When  is causal, this definition reduces to the usual (unilateral) DTFT definition:
is causal, this definition reduces to the usual (unilateral) DTFT definition:
Applying this relation to  gives
gives
Thus, the spectrum of the filter output is just the input spectrum times the spectrum of the impulse response  . We have therefore shown the following:
. We have therefore shown the following:
This immediately implies the following:
We can express this mathematically by writing
By Eq. (7.2), the frequency response specifies the gain and phase shift applied by the filter at each frequency. Since
(7.2), the frequency response specifies the gain and phase shift applied by the filter at each frequency. Since  ,
,  , and
, and  are constants, the frequency response
are constants, the frequency response  is only a function of radian frequency
is only a function of radian frequency  . Since
. Since  is real, the frequency response may be considered a complex-valued function of a real variable. The response at frequency
is real, the frequency response may be considered a complex-valued function of a real variable. The response at frequency  Hz, for example, is
Hz, for example, is  , where
, where  is the sampling period in seconds. It might be more convenient to define new functions such as
is the sampling period in seconds. It might be more convenient to define new functions such as  and write simply
and write simply  instead of having to write
instead of having to write  so often, but doing so would add a lot of new functions to an already notation-rich scenario. Furthermore, writing
so often, but doing so would add a lot of new functions to an already notation-rich scenario. Furthermore, writing  makes explicit the connection between the transfer function and the frequency response.
makes explicit the connection between the transfer function and the frequency response.
Notice that defining the frequency response as a function of  places the frequency ``axis'' on the unit circle in the complex
places the frequency ``axis'' on the unit circle in the complex  plane, since
plane, since  . As a result, adding multiples of the sampling frequency to
. As a result, adding multiples of the sampling frequency to  corresponds to traversing whole cycles around the unit circle, since
corresponds to traversing whole cycles around the unit circle, since
whenever  is an integer. Since every discrete-time spectrum repeats in frequency with a ``period'' equal to the sampling rate, we may restrict
is an integer. Since every discrete-time spectrum repeats in frequency with a ``period'' equal to the sampling rate, we may restrict  to one traversal of the unit circle; a typical choice is
to one traversal of the unit circle; a typical choice is  [
[  ]. For convenience,
]. For convenience, ![$ \omega T \in[-\pi,\pi]$](file:///C:\DOCUME~1\ADMINI~1\CONFIG~1\Temp\msohtmlclip1\01\clip_image033.gif) is often allowed.
is often allowed.
We have seen that the spectrum is a particular slice through the transfer function. It is also possible to go the other way and generalize the spectrum (defined only over the unit circle) to the entire  plane by means of analytic continuation (§D.2). Since analytic continuation is unique (for all filters encountered in practice), we get the same result going either direction.
plane by means of analytic continuation (§D.2). Since analytic continuation is unique (for all filters encountered in practice), we get the same result going either direction.
Because every complex number  can be represented as a magnitude
can be represented as a magnitude  and angle
and angle  , viz.,
, viz.,  , the frequency response
, the frequency response  may be decomposed into two real-valued functions, the amplitude response
may be decomposed into two real-valued functions, the amplitude response  and the phase response
and the phase response  . Formally, we may define them as follows:
. Formally, we may define them as follows:
Frequency Response Ranges
You will often see frequency response quoted as a range between two figures. This is a simple (or perhaps "simplistic") way to see which frequencies a microphone is capable of capturing effectively. For example, a microphone which is said to have a frequency response of 20 Hz to 20 kHz can reproduce all frequencies within this range. Frequencies outside this range will be reproduced to a much lesser extent or not at all.
This specification makes no mention of the response curve, or how successfully the various frequencies will be reproduced. Like many specifications, it should be taken as a guide only.
HENDERSON PARADA

thanking for you giving this wonderful opportunity <a href="http://www.civiltech321blogspot.com>best education blog <a>
ResponderEliminar<a href="http://civiltech321blogspot.com>
ResponderEliminar